Análise de experimento – Dinâmica

Colégio Pedro II – Campus Centro

Matéria: Física      Professor: Sérgio Ferreira de Lima

Alunos: Caio Gentil                                  nº.: 02                   Turma: 1203

João Marcos                                              nº.: 15

Leonardo Cattari                                      nº.: 21

Leonardo Sayão                                         nº.: 22

 

Introdução

 

Neste ano de 2015 os alunos do segundo ano do ensino médio começaram a estudar cinemática e as Leis de Newton (dinâmica). No dia,foi feito um experimento no laboratório de física, a fim de que os alunos possam aprender de uma maneira diferente alguns conceitos relacionados à cinemática e às Leis de Newton (dinâmica).

 

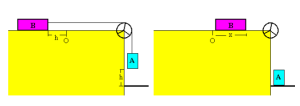
O experimento consiste em um sistema composto por dois corpos (A e B), uma roldana e um fio/corda/cabo. Como ilustra a figura o corpo B pode ficar em cima de uma mesa e preso ao corpo A pendurado pela roldana na parte de fora da mesa. A massa de A fará com que o corpo A se desloque para baixo com aceleração “a” e percorrerá a distância “h”. Do mesmo jeito, (mas horizontalmente) por causa da massa de A, o corpo B vai acelerar para a direita com a mesma aceleração “a” e vai percorrer a mesma distância “h”, mas devido à inércia do movimento de B (um corpo que está em movimento tende a continuar em movimento até que outra força atue sobre ele) ele vai continuar seu movimento da esquerda para direita com aceleração retardada (freando) “ a’ “ até que a força de atrito o pare, tendo percorrido a mais que “h” a distância “x”. Será medido o tempo “t” do deslocamento de A até o chão.

 

Dado o funcionamento do experimento foram estipulados como objetivos pelo professor:

• Determinar o coeficiente de atrito cinético;
• Comparar aceleração teórica com a experimental;
• Analisar a propagação de erros em experimentos.

 

Para atingirmos esses objetivos vamos:

1. Usar as Leis de Newton para deduzir (a) em função da massa de A, massa de B e g (aceleração da gravidade);P – T = Ma x aMa.g – T = Ma x a 

   T – Fat = Mb x a

   T – µ.Mb.g = Mb x a

   Somatório da Equações:

   Ma.g – µ.Mb.g = Mb x a + Ma x a

   g(Ma – µ.Mb) = a(Mb + Ma)

   a = g(Ma – µ.Mb / Mb + Ma)

2. Usar a Equação de Torricelli para deduzir a velocidade de B quando A toca o chão; Distância hVo = 0Vf = ?

   a = g(Ma – µ.Mb / Mb + Ma)

   Então,

   Vf² = Vo² + 2.g.h.a

   Vf² = 2.g.h.(Ma – µ.Mb / Mb + Ma)

3. Usar as Leis de Newton para deduzir (a’) em função da massa de B e do coeficiente de atrito μ;Fat = Mb.a’µ.Mb.g = Mb.a’a’ = µ.g
4. Escrever as equações do Movimento Uniformemente Variado (MUV) para a massa B até parar, percorrendo a distância (x)função horária da velocidadeV = Vo – at0 = Vf _{trecho h}– µ.g.t

   Função horária da posição

   ΔS = Vo.t – at²/2

   x = Vf _h.t – µ.g.t²/2

5. Isolar o “t” (tempo) da equação de velocidade e substituir na equação de posição;Função horária da velocidadeV = Vo – at0 = Vf – µ.g.t

   t = Vf _h/ µ.g  (função da aceleração do trecho x com o t isolado)

6. Substituir a velocidade final do primeiro movimento na inicial do segundo movimento;Função horária da posiçãoΔS = Vo.t – at²/2X = Vf_h.t – µ.g.t²/2 → Função da posição no trecho x

   X = Vf _h.Vf _h/ µ.g – µ.g/2.(Vf/ µ.g)²

   X = Vf ² _h/ µ.g – Vf² _h/2. µ.g

   X = Vf² _h/2. µ.g

7. Reescrever a equação para que μ fique em função de massa de A (Ma), massa de B (Mb), x e h.x = 2.g.h.(Ma – µ.Mb / Mb + Ma) / 2. µ.gx = H/m.(Ma – µ.Mb / Mb + Ma)µ = h/x.(Ma – µ.Mb / Mb + Ma)

   µ = Ma.h – µ.Mb.h / Mb.x + Ma.x

   µ.Mb.x + µ.Ma.x = Ma.h – µ.Mb.h

   µ.Ma.x + µ.Mb.x + µ.Mb.h = Ma.h

   µ (Ma.x + Mb.x + Mb.h) = Ma.h

   µ = Ma.h / Ma.x +Mb.x +Mb.h

    

   µ = Ma.h / x(Ma + Mab) + Mb.h  (equação de μ em função Ma, Mb, x. e h)

8. Deduzir a expressão da aceleração de queda em função de (h) e (t);Função horária da posiçãoΔS = Vo.t + at²/2h = at²/2

   a = 2h/t² (equação da aceleração em função de h e t)

9. Comparar o valor de “a” cinemático com o valor de “a” teórico.

 

Dados coletados no experimento:

• Ma = (85g ± 1g)
• Mb = (105g ± 1g)
• H= (0,44m ± 1m)
• x = (0,52m ± 1m)
• t = (0,442s ± 0,001s)

Dados já conhecidos:

• Aceleração da gravidade – g = 9,8 m/s²

Termos que serão usados nas equações que não foram explicitados acima:

• Fat = Força de atrito
• T = Força de tração
• V = velocidade

 

Cálculo do coeficiente de atrito (µ)

µ = Ma.h / x(Ma + Mab) + Mb.h

µ = 85 +- 1 . 44 +- 0.1 / ( 85 +- 1 + 105 +- 1) 52 +- 0.1 + 105 +- 1 . 44+- 0.1

µ= 3748 +- 52.5 / 14500 +- 177.5

µ= 0.2584 +- 0.0067

 

Cálculos

Acelerações de H 

Teórica:

a = g( Ma- µ . Mb)/ Ma+ Mb

a =9.8 (85-0.26 . 105)/ 105 + 85

a = 9.8 . 57.7 / 190

a = 2.9761 m/s²

Experimental:

A = 2h/t²

A = 0.88 +- 0.01/ 0.195364 +- 0.000884

A= 4.5044 +- 0.071 m/ s²

 

Comparações entre as acelerações (teórica e prática)

Encontramos grande diferença entre as duas acelerações. Esse fato acontece devido as imprecisões que acontecem no experimento como: a falta de instrumento com alta precisão para captar os valores de forma precisa; arredondamento durante os cálculos para que se ache uma resposta mais coerente; etc. Sendo assim, ao chegar no resultado final, encontra-se uma grande diferença entre os resultados.