RELATÓRIO SOBRE O EXPERIMENTO DOS BLOCOS – 2ª CERTIFICAÇÃO

Colégio Pedro II – Campus Centro

Física – Professor: Sérgio Lima

Integrantes: Leonardo Barbosa de Oliveira nº:15

Lucas Oliveira Pinhel nº :19                                     TURMA:1207

O Trabalho:

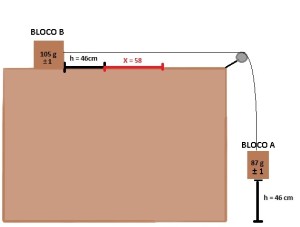
O trabalho consistia em um experimento onde dois corpos “A” e “B” estavam presos por um fio ligado em uma roldana. O corpo “A” estava pendurado para fora da mesa, suspenso pelo fio que passava pela roldana e ligava-o no corpo “B” que se encontrava em cima da mesa.

Soltando o peso que prendia o bloco “B”, este era arrastado pelo fio numa distância h (que é a mesma distancia de “A” para o chão). Quando o bloco A toca o chão, o bloco B ainda continua se movendo, porém agora freando (devido a força de atrito). Este deslocamento é chamado de X. O bloco “A” cai no chão com a distancia h com a mesma aceleração que o bloco “B” percorre h na mesa. Depois, o bloco B freia em X com uma aceleração “ a’ ”.

Medidas:

Para fazer as medidas foram utilizados duas réguas milimetradas e um cronômetro. As medidas não são exatas, pois toda tem um erro. O erro na régua é 1 mm e no cronômetro 0,01s.  As medidas do experimento são:

Massa bloco A = (87 ± 1)g

Massa bloco B = (105 ±1) g

h= (46 ± 0,01)cm = (0,46 ± 0,001)m

X= (58 ± 0,01)cm = (0,58 ± 0,001)m

Tempo (t) = (0,404 ± 0,01) m/s

 

Nesta certificação, o objetivo do trabalho na verdade são três:

• Determinar o coeficiente de dilatação cinético (µ)
• Obter e comparar a aceleração teórica (Ateor) e a aceleração experimental (Aexp)
• Analisar a propagação de erro no experimento.

 

1 – DETERMINAR µ

Para se determinar µ, o coeficiente de atrito, usamos a seguinte equação:

µ= (Ma . h) / (Ma + Mb) . x + Mb . h

Porém, para se chegar nesta equação, é preciso fazer outras equações que levam à ela. Vamos lá?

1.1 – Usar a equação de Torricelli para deduzir a velocidade do bloco B quando o bloco A toca no chão.

V²=V0² + 2.a. Δs

V²=2.h . (Ma – µ . Mb/Ma + Mb).g

mais adiante entenderemos por que a = (Ma – µ . Mb/Ma + Mb).g

V²=2.h.g(Ma – µ . Mb/Ma + Mb)

1.2 – Usar as leis de Newton para deduzir a’ em função de Mb e µ

2ª Lei de Newton: Fr = m.a

µ . Mb . g = Mb . a’

a’= µ.g

1.3 – Escrever as equações do MUV (movimento uniformemente variado) para Mb até parar percorrendo a distância x:

X= V0t – (µ.g.t²/2)

&

0=V0 – µ.g.t

1.4 – Isolar o t da equação da velocidade e substituir na equação da posição:

V= µ.g.t

t=V/ µ.g

x= (V.V/ µ.g) – (µ.g/2) . (V²/ µ².g²)

x= (V²/ µ.g) – (V²/2. µ.g)

x=V²/2. µ.g

1.5 – Substituir a velocidade final do primeiro movimento na inicial do segundo movimento:

x= (2.h.g.(M- µ.Mb/Ma+Mb))/2.µ.g

1.6 – Reescrever a equação para que µ fique em função de Ma, Mb, x e h:

x=(h/ µ) . (Ma- µ.Mb/Ma + Mb)

µ= (Ma . h) / (Ma + Mb) . x + Mb . h

Pronto, agora podemos descobrir µ.

Substituindo os termos temos e colocando seus respectivos erros:

µ=   (87 ± 1) . (0,46 ± 0,001)/((87 ± 1) + (105 ± 1)).(0,58 ± 0,001) + (105 ± 1) . (0,46 ± 0,001)

E resolvendo a equação encontra-se:

µ=     (40,02 ± 0,547)/ ((192 ± 2) . (0,58 ± 0,001)) + (48,3 ± 0,565)

µ=     (40,02 ± 0,547)/  (111,36 ± 1,352) + (48,3 ± 0,565)

µ=     (40,02 ± 0,547)/  (159,66 ± 1,917)

µ=  (0,2506576475 ± 0,0064354)   ≅ 0,251 ± 0,006

 

Vemos que o coeficiente de atrito cinético, neste caso, é aproximadamente 0,251

 

2 – OBTER ACELERAÇÃO TEÓRICA E ACELERAÇÃO EXPERIMENTAL E COMPARÁ-LAS

Aceleração teórica:

Para se obter a aceleração teórica utilizamos a segunda lei de Newton -> Fr=m.a

mA . g – T = mA . a           -> corpo A

T – µ . mB . g = mB . a      -> corpo B

mA . g – µ . mB . g = (mA + mB) . a

a = g (mA – µ . mB) / mA + mB     * não falei que entenderíamos?*

Substituindo…

a= 9,8 ((87 ± 1) – (0,251 ± 0,006) . (105 ± 1))/ (87 ± 1) + (105 ± 1 )

a= 9,8 (60,645 ± 1,881)/ (192 ± 2)

a= 9,8 ( 0,315 ± 0,01)

a= 3,087 m/s²

 

Para se obter a aceleração experimental usamos: a= 2.h/t²

aexp= 2. (0,46 ± 0,001)/( 0,404² ± 0,01)

aexp=  (0,92 ± 0,001)/ (0,17 ± 0,01)

aexp= (5,4 ± 0,3)

aexp= 5,4 m/s²

A aceleração teórica é menor do que a aceleração experimental, e isso se de pelo fato de…

 

3 – ANALISAR A PROPAGAÇÃO DE ERRO NO EXPERIMENTO.

É nítida a diferença entre a aceleração teórica e a aceleração experimental. Isso se dá pelo fato de que nenhuma medida, utilizando-se dos instrumentos usados no experimento, é 100% correta, por conta das incertezas neles contidos. Sem contar os arredondamentos nas contas para facilitá-las (e para torná-las possíveis pois muitos números eram dízimas), e outros fatores também como deformidades na mesa e nos blocos, pressão exercida pelo ar e entre outros.

 Obs: Professor, só consegui postar agora por conta do motivo que te disse.