Roteiro do Experimento de Física da 2ª Certificação

COLÉGIO PEDRO II – CAMPUS CENTRO
Professor: Sérgio Lima
Alunxs: Anna Clara (n° 03)
Camila Ribeiro (n° 08)
Gabriella Frazão (n° 13)
Nathalia Sartore (n° 30).
Turma: 1205

ANÁLISE DO EXPERIMENTO

 

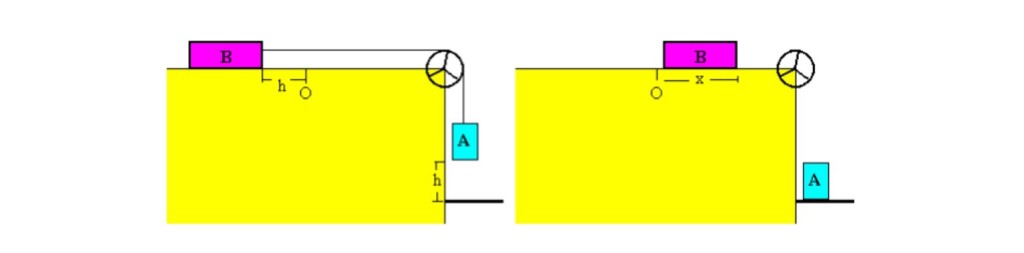
No dia 16 de julho, realizamos um experimento no laboratório de Física que buscava analisar o que acontecia com dois blocos; o bloco B estava apoiado em cima da mesa, sendo bloqueado por um peso e amarrado a uma corda que passava por uma roldana e que se prendia a um outro bloco A. O experimento ocorreu de forma que o peso era imediatamente retirado de cima do bloco e o liberava, percorrendo em um determinado tempo e com uma determinada aceleração uma distância h, que é a mesma distância do bloco A até o chão. Após o bloc A atingir o chão, o bloco B aimda percorre uma distância x, como está representada na figura abaixo.

 

 

Os instrumentos utilizados nesse processo foram:

. Uma régua para medir a altura do Bloco A até o chão e também a distância que ele se deslocava após a aceleração;
. Uma corda que prendia os dois blocos;
. Um cronômetro que calculava o tempo em que o Bloco A atingia o chão;
. Um peso de massa x para prender o bloco B;
. Uma roldana por onde a corda passava e estava presa ao bloco A;
. E uma balança para medir o peso dos blocos.

Nas imagens a seguir, é mostrado o passo a passo da experiência realizada:

Inicialmente, tivemos a ajuda de um instrutor que nos ajudou a calcular as massas dos dois blocos usados em uma balança. Depois, medimos a altura h do bloco A com o auxílio de uma régua.

Na imagem abaixo podermos ver o bloco B sendo bloqueado por um certo peso e sensores que se ligavam ao cronômetro para indicar o intervalo de tempo do percurso do em que o bloco B percorre a distância h.

 

Após o bloco B percorrer a distância h, ele ainda caminha uma distância x também medida com o auxílio de uma régua.

 

Após a medição no laboratório, com o auxílio de instrumentos, achamos os valores iniciais necessários para aplicarmos nas fórmulas, ou seja, as medidas diretas. E acrescentamos às medidas seus respectivos erros experimentais.

Estas foram:
Massa do bloco A: 85 g ± 1 (pesado na balança)
Massa do bloco B: 105 g ± 1 (pesado na balança)
Altura (h) do bloco A até o chão: 46,4cm ± 0,1 (lido na régua)
Tempo: 0,406 milésimos (lido no cronômetro)
Distância que o bloco B anda depois do Bloca A atingir o chão (x) = 61,0 cm ± 0,1 (lido na régua)

 

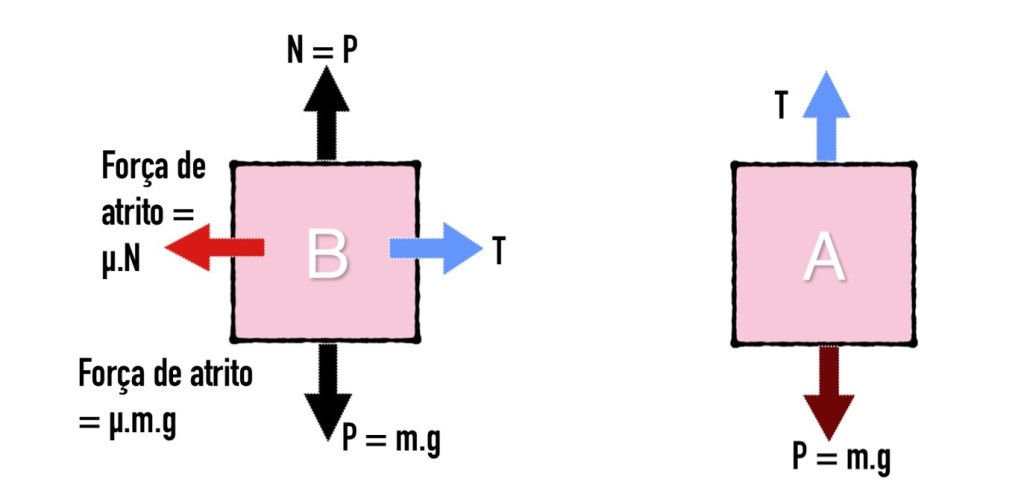
Ao analisar o experimento utilizaremos a 2° lei de Newton, já que os objetos estarão em movimento: Soma das forças (F)= massa x aceleração. Como objetivo do trabalho buscaremos encontrar o valor da aceleração do sistema, e para isso, também o valor do coeficiente de atrito.

Sendo:
T = tração dos fios assinalados na imagem
μ = coeficiente de atrito cinético ( nossa incógnita)
mb = massa do bloco B
ma = massa do bloco A
g = valor gravitacional = 10 m/s²

Soma das forças do bloco B: T-  μ . mb . g = mb . a
Soma das forças do bloco A: ma . g – T + ma . a

O sistema fica então:
T-  μ . mb . g = mb . a
ma . g – T + ma . a

Após deduzi-la, obtém-se a equação: a = g . (ma – μ . mb) / (ma + mb)
Esta é a equação da aceleração teórica que usaremos para comparar com o valor da aceleração real. Porém, não temos ainda o valor do coeficiente (μ), por isso descobriremos primeiro este e depois retornaremos neste ponto.

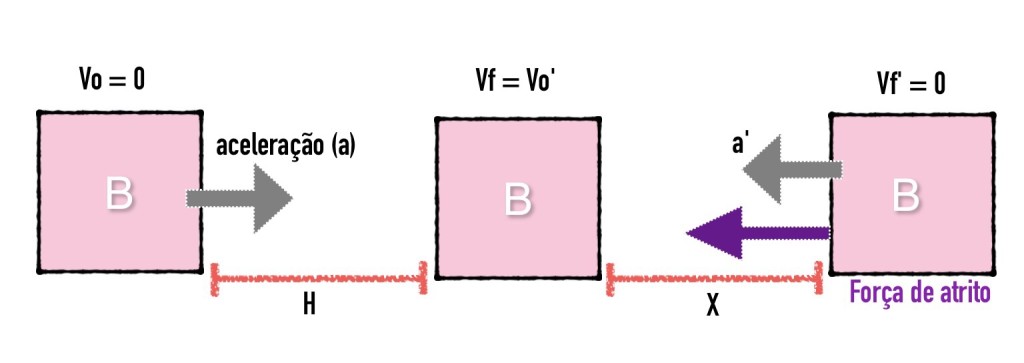
Na segunda parte desta situação, quando o bloco B anda uma distância x além da h, descobriremos a aceleração (a’) e a velocidade final ( Vf = Vo’). Os dois serão substituídos na fórmula do movimento uniformemente variado, já que ele desacelera com passar do tempo diminuindo sua velocidade até parar. Observe:

Descobrindo o valor de a’:
F = m. a’
Fat= mb. a’
g. mb. μ= mb . a’
a’= μ . mb. g/ mb
a’ = μ . g

Depois usamos Torricelli para descobrir a velocidade final (Vf = Vo’)
Torricelli: Vf2 = Vo2 + 2. a . ΔD
Vf2 = 0 + 2 . ( g. (ma – μ . mb)/ ma + mb) .h
Vf2 = 2 . h . g (ma – μ . mb) / ma+ mb)
E, por último, a equação do m.u.v:
S= So + Vo’t + at2/2
ΔS = Vo’t + at2/2

Substituindo:
ΔS -> x (quanto a mais o bloco B andou depois de já ter corrido a distância h)
a (aceleração) -> a’= μ . g
t (tempo) ->
V(t) = Vo + at
Vf’ = Vo’ – μ . g . t
0 = Vo’ – μ . g . t
t= Vo’ / μ . g

Ficará, então:
x= Vo’.t – μ .g.t2/2
x= Vo’ . Vo’ / μ. g + μ. g/ 2 . (Vo’2 / μ2 . g2)
x= Vo’.Vo’/ μ.g – μ.g . Vo’2/ μ
x= Vo’2 / .g – Vo’2 / 2. μ.g
x= Vo’2 / 2. μ. g

Substituindo aqui o valor de Vf = Vo’ = Vf2 = 2 . h . g (ma – μ . mb) / ma+ mb)
x = 2.h.g.(ma – μ . mb/ ma + mb)/ 2. μ.g
x= (ma – μ . mb) .h/ (ma + mb) . μ

Concluindo…
μ = ma.h/ (ma + mb) .x + mb.h

Substituimos os valores encontrados no dia do experimento:

μ = (85 . 46,4) / (85 + 105) . 61 + 105 . 46,4

μ =   3944/ 190 . 61 + 105 . 46,4

μ = 3944/ 11590 + 4872

μ = 3944 / 16462

μ= 0,2395820678

μ é aproximadamente 0,24

 

 

A partir do valor de μ, podemos calcular a aceleração teórica com a fórmula: a = g . (ma – μ . mb) / (ma + mb) substituindo os valores:

a = 10. ( 85 – 0,24 . 105) / 85 + 105

a= 10 . (85 – 25,2) / 190

a= 598/ 190

aceleração teórica é aproximadamente 3,15 m/ s2 

 

Com o valor da aceleração teórica, podemos comparar com o da aceleração real, pois na teórica não conta com algumas interferências do meio. É possível calcular a real através da fórmula:

ΔS = Vo’t + at2/2

h = 0.t + at2/2

a = 2h/t2

a = 2. 0,464/ 0,4062

Então: aceleração real =  5,62 m/ s2 

Para analisarmos a propagação de erros, utilizamos a fórmula já usada anteriormente para descobrir o valor de μ, só que incluindo seus erros experimentais. Desse modo, fica assim:

μ = ( 85 ± 1 . 46,4 ± 0,1) / (85 ± 1 + 105 ± 1) . (61,0 ± 0,1) + (105 ± 1 . 46,4 ± 0,1)
μ = (3944 ± 54,9) / (190 ± 2) . (61,0 ± 0,1) + (4872 ± 56,9)
μ = (3944 ± 54,9) / (11590 ± 141) + (4872 ± 56,9)
μ = (3944 ± 54,9) / (16462 ± 197,9)
μ = 54,9/ 16462 + (3944/ 164622) . 197,9 -> dD= [dA/B + (A/B2). dB]
μ = 0,2395820679 ± 0,0062151191
μ é aproximadamente 0,23958 ± 0,00621.

Ou seja, seu erro ficou em aproximadamente 0,00621.