Colégio Pedro II – Campus Centro
Disciplina: Física
Professor: Sérgio Lima
Grupo: Bernardo Maia Nº: 6
Breno Cipolatti Nº: 7
Felipe Pais Nº: 9
José Victor Nº: 17
No dia 16/07 a turma fez um experimento no laboratório de física, com a intenção de examinar fenômenos que consistem em velocidade, peso, atrito e aceleração.
Foram usados objetos comuns, como blocos de madeira, linha e um pequeno peso de ferro, também foi utilizado um equipamento eletrônico, um cronometro de alta precisão, que era composto pelo mostrador (onde mostra o tempo) e dois “retângulos” vazados que contêm um laser cada, que inicia e para o cronometro quando um objeto passa por eles.
Devemos descobrir o coeficiente de atrito cinético, comparar a aceleração teórica com a experimental e analisar a propagação de erros no experimento.
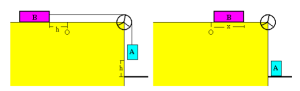
O primeiro passo é descobrir a aceleração teórica. Para isto, deve-se usar os seguintes passos:
Fat = μ · N ou Fat = μ · Mb · g
Ma · g – T = Ma · a +
T – μ · Mag = Mb · g
Ma · g – μ · Mb · g = (Ma + Mb) a
a = Ma · g – μ · Mb · g —–> (Ma – μ · Mb) · g
Ma + Mb Ma + Mb
Agora é só substituir pelos números dados. Porém ainda necessitamos descobrir μ (coeficiente de atrito), em uma conta separada.
Devemos usar a fórmula:
μ = (0,085 ± 0,001 · 0,457 ± 0,01)/(0,085 ± 0,001 + 0,105 ± 0,001) · 0,504 ± 0,01 + 0,105 ± 0,001 · 0,457 ± 0,01
μ = 0,039 ± 0,0013/(0,190 ± 0,002 · 0,504 ± 0,01) + (0,105 ± 0,001 · 0,457 ± 0,01)
μ = 0,039 ± 0,0013/0,096 ± 0,003 + 0,048 ± 0,0015
μ = 0,039 ± 0,0013/0,144 ± 0,0018
μ = 0,27 ± 0,0125
Feito isso, só substituir as letras por números:
Fat = μ · N ou μ · Mb · g
Fat= 0,27 ± 0,017 · 105 ± 1 · 9,8
Ma · g – T = Ma · a +
T – μ · Mb · g = Mb · a
0,085 ± 1 · 9,8 – T = 0,085 ± 1 – a
T – 0,27 ± 0,017 · 0,105 ± 1 · 9,8 = 0,105 ± 1 · a
(0,085 ± 0,001 · 9,8) – (0,27 ± 0,0073 · 0,105 ± 0,001 · 9,8) = ( 0,085 ± 0,001 + 0,105 ± 0,001) · a
( 0,085 ± 0,001 · 9,8) – ( 0,27 ± 0,0073 · 0,105 ± 0,001· 9,8) = 0,190 ± 0,002 · a
a = ( 0,085 ± 0,001 · 9,8) – ( 0,27 ± 0,0073 · 0,105 ± 0,001 · 9,8)
0,190 ± 0,002
a = 9,8 ( 0,085 ± 0,001 – 0,27 ± 0,0073 · 0,105 ± 0,001)
0,190 ± 0,002
a = 9,8 ( 0,085 ± 0,001 – 0,028 ± 0,001)
0,190 ± 0,002
a = 9,8 (0,057 ± 0,002)
0,190 ± 0,002
a = 0,56 ± 0,002
0,190 ± 0,002
a = 2,95 ± 0,041 m/s²
Esta aceleração está em função das massas
Agora, deve-se descobrir a aceleração experimental:
a = 2h /t²
a = (2 · 0,457 ± 0,01)/(0,410 ± 0,01)²
a = 0,914 ± 0,01/0,17 ± 0,0001
a = 5,38 ± 0,063 m/s²
Foi observado que a aceleração experimental foi maior que a teórica.
Agora, deve-se descobrir a velocidade de do bloco B quando o bloco A toca o chão. Para isto, devemos usar a equação de Torricelli, com as duas acelerações:
Vf² = Vo² + 2 · a · ΔS
Vf² = 2 · H · a
Vf² = 2 · 45,7 ± 1 · 2,95 ± 0,041 Vf² = 2 · 45,7 ± 1 · 5,38 ± 0,063
Vf² = 91,4 ± 1 · 2,95 ± 0,041 Vf² = 91,4 ± 1 · 5,38 ± 0,063
Vf² = 269,6 ± 6,7 Vf² = 491,7 ± 11,1
Vf = √269,6 ± 6,7 Vf = √491,7 ± 11,1
Agora que descobrimos a velocidade em que o bloco B percorre a distancia H, devemos, usando as leis de Newton, descobrir a aceleração dinâmica, que é a aceleração que o bloco B tem após o bloco A tocar o chão, em função de μ e Mb:
Aceleração dinâmica: Aceleração cinemática:
Fr = Fat
μ ·Mb · g = Mb · a’ a’ = x/a.h
a’ = μ · g a’ = 0,504 ± 0,01/5,38 ± 0,063 · 0,457 ± 0,01
a’ = (0.27 ± 0,0073) · 9,8 a’ = 0,504 ± 0,01/2,46 ± 0,082
a’ = 2,65 ± 0,0073 m/s² a’ = 0,2 ± 0,01 m/s²
A aceleração dinâmica foi bem maior que a cinemática.
Em seguida, usando as equações do MUV para a massa até parar percorrendo a distância x:
Δ S= Vo · T – a‘T²/2
X = Vo · T – μgT²/2
Agora devemos isolar o T da equação da velocidade e substituímos na equação de posição:
V = Vo – aT
0= Vo – μgT
Vo = μgT
T = Vo/ μg
X= Vo · Vo/μg – μg/2 · (Vo/μg)²
X= Vo · Vo/μg – μg/2 · Vo²/μ² g²
X= Vo²/μg – Vo²/2μg
X= Vo²/2μg
X= Vo² / 2 · 0,27 ± 0,0073 · 9,8
Vo² = Vf², pois a velocidade que ele começa a percorrer o espaço X é a mesma que ele termina de percorrer o espaço H. Entã só devemos substituir Vo² pela fórmula do Vf²:
X = 2 · H · a /2μg
X = 2 · H · a /2μg Obs: a = (Ma – μ · Mb) · g / (Ma + Mb)
X = H · [(Ma – μ · Mb) · g /(Ma + Mb)] / μg
X = H · [(Ma – μ · Mb) · g/(Ma + Mb)] / μg
X = H · [(Ma – μ · Mb)/(Ma + Mb)] / μ
Xμ = H · (Ma – μ · Mb)/(Ma + Mb)
(Ma + Mb) · Xμ = H · (Ma – μ · Mb)
(Ma + Mb) μX = HMa – Hμ·Mb
(Ma + Mb) μX + Hμ·Mb = HMa
Xμ + Hμ·Mb = (HMa)/(Ma+ Mb)
μ (X + HMb) = (HMa)/(Ma+ Mb)
μ = (HMa)/(Ma + Mb)X + HMb







