Colégio Pedro II – Campus Centro
Alunos: Bruno Gentil nº.:07
Felipe Castro n.:11
João Izel n.:14
Júlia Pimentel n.:15
Análise de experimento – Dinâmica
O experimento consiste em 3 partes:
1) A análise das medidas
2) O cálculo teórico
3) O cálculo experimental
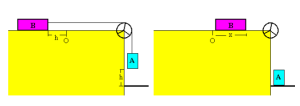
Na primeira etapa medimos, com a régua, a altura do objeto pendurado (h). Logo após, medimos X. Foi dada a massa dos blocos (Ma e Mb) e quando o peso que estava em cima do bloco B foi retirado calculamos o tempo (t) que o bloco A demora pra tocar no chão.
Na segunda parte fizemos o calculo teórico (sem as medidas) para descobrir a equação do µ
Por fim, substituímos as medidas na equação achando o coeficiente de atrito (vulgo µ) e as acelerações.
-MEDIDAS:
ma = 85g ± 1g
mb = 105g ± 1g
h = 46 cm x = 67,5 cm
t = 0,429 s
-CÁLCULOS TEÓRICOS (equações de µ e das acelerações)
1) Leis de Newton – Descobrindo (a)
ma . g – T= ma . a
T – µ . mb . g = mb . a
ma . g – µ . mb . g = (ma + mb) . a
logo, temos que:
a= g(ma – µ . mb) / (ma + mb)
2) Torricelli
Descobrindo Velocidade (V) de B quando A toca o chão
Vf²= Vo² ± 2aΔs
Vf²= 2gh (ma – µ . mb) / (ma – mb)
3) Leis de Newton
Descobrindo (a’)
Fat= µ . N
Fat= mb . a’
µ. mb. g= mb . a’
a’= µg
4) Equações de MUV
Descobrindo X
V= Vo – at
0= Vo – µg . t
logo,
t= Vo / µg
S= So – vt – at²/2 (substituindo t por Vo/µg)
e sabendo que, S-So=X (distância)
temos que: X= Vo’ t – µg t²/2
X= Vo’ . Vo’/µg – µg/2 . (Vo²/ µ²g²)
X=Vo’²/ µg – Vo²/2 µg
X= Vo²/2 µg (substituindo Vo² pelo Vf² )
X= (2gh / 2ug) . [(ma – µ . mb) / (ma – mb)]
X= (ma- µ. Mb)h / (ma + mb)µ (colocando µ em evidência)
µ= (ma- µ. Mb)h / (ma + mb)X
CÁLCULOS COM AS MEDIDAS EXPERIMENTAIS
µ= ma . h/(ma+mb) . x + mb . h
µ= (85 ± 1). 46 + 0,1/[(85 ± 1) + (105 ± 1)]. 67,5 ± 0,1 + 105 + 1 . 46 ± 0,1
µ= 3910/190 67,5 + 105. 46
µ= 3910/12825 + 4830
µ= 3910/17655
µ= 0,22 ± 0,07
Aceleração Teórica
a= g ( ma – µ.mb) / ma + mb
a= 9,8 (85 – 0,22 . 105) / 85 + 105
a= 9,8 (85 – 23,1) / 190
a= 9,8 (61,9) / 190
a= 3,2 aproximadamente
Aceleração experimental com base na equação de Torricelli
v²= v0² + 2aΔS
Após desenvolver fica:
a= 2h/ t²
a= 0,92/0,184041
a= 4,99
a=5