Colégio Pedro II – Campus Centro
Experimento de Física – Profº Sérgio
Componentes : Fabiano Ferreira nº 09 Turma 1201
Miguel Hauer nº 25
Nathalia Oliveira nº 26
Yasmin Passoumidis nº 30
Yasmin Hughes nº 31
O EXPERIMENTO
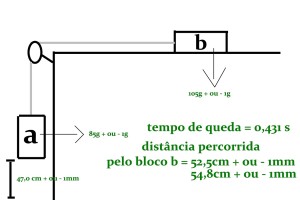
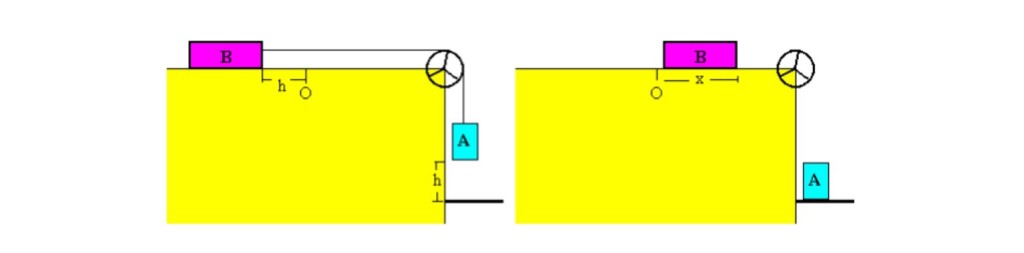
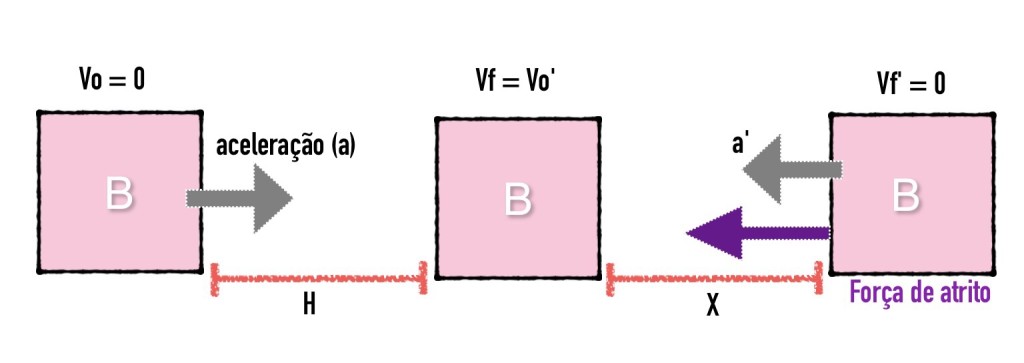
Há dois blocos A e B de massas conhecidas.O bloco B, de massa 105 g +/- 1g, fica em cima da mesa com um peso em cima dele, segurando-o e o bloco A, de massa 85g +/- 1g, fica suspenso por uma corda que transpassa uma roldana.Tira-se o peso do bloco B, este se desloca pela mesa com a mesma aceleração a em que o bloco A toca no chão, ambos percorrem uma distancia h. Esta foi medida com uma fita métrica,bem como a distância x medida com uma régua e o tempo t registrado pelo cronômetro disponibilizado.Após o bloco A cair por completo, o bloco B anda mais uma nova distância x, freando com uma nova aceleração a´ devido a força de atrito que atua no mesmo.Os objetivos desse experimento são: determinar o coeficiente de atrito cinético da mesa – em função da massa, da gravidade e da distância -, comparar a aceleração teórica/experimental e analisar a propagação de erros em experimentos.
Para calcular a primeira aceleração a (de queda), deduzimos a em função de ma, mb e g, usando as leis de Newton. Essa aceleração é a do experimento(dinâmica).
Analisando cada bloco em separado, temos que:
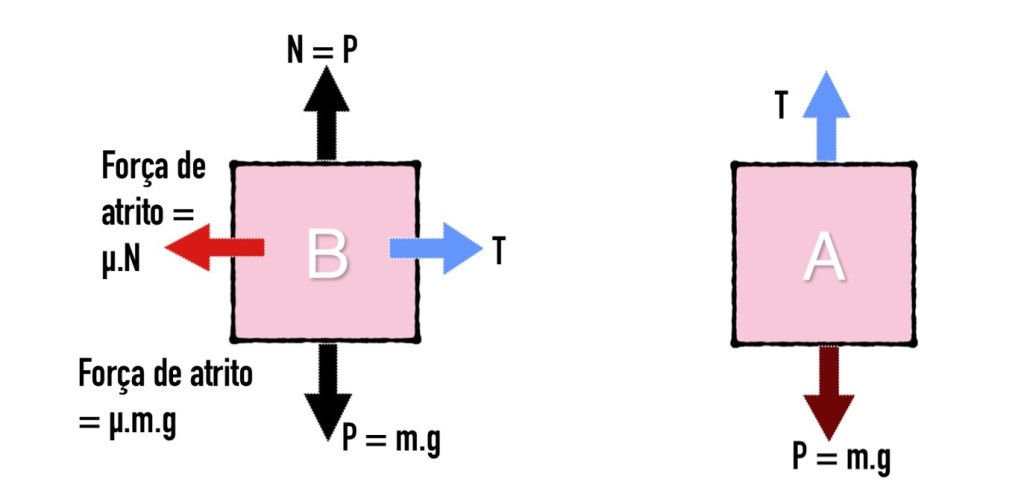
1) No bloco B, há a força P e N de mesmo módulo mb.g, a força T de tração da corda e uma força de atrito Fat de módulo μ.m.g
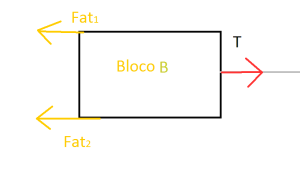
2) No bloco A, há duas forças, a tração T(mesma de B) e a P de módulo ma.g
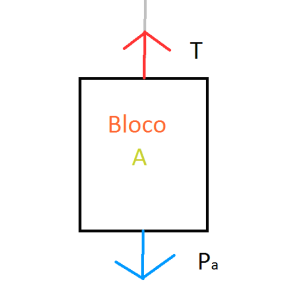
Aplicando a 2ª Lei de Newton para cada massa:
ma. g – T = mb. a
T- µ.mb.g=mb.a
ma.g- µ.mb.g=(ma+mb)a
g(ma- µ.mb)=(ma+mb)a
a=g(ma- µ.mb)/ma+mb
Para calcular a velocidade do bloco B quando o bloco A toca o chão, usamos a Equação de Torricelli:
V²=0²+2.a.h
V²=2.a.h
Escrevemos as equações do MUV para a massa até parar percorrendo a distância x.
Vf²= 2.g.h (ma- µmb/ma+mb)
Continuando ainda em Torricelli:
0²=Vo²-2.a´.x
0=2ah-2a´x
a´= x/ah (cinemática)
Usamos também a Lei de Newton para deduzir a’ (aceleração retardatória de B até este parar) em função de mb e µ
µ. mbg = mb. a’
µ. mb. g/mb = a’
a´= µ.g(dinâmica)
Isolamos o t da equação da velocidade e substituímos na equação de posição.
a= (ma- µ.mb)/ma + mb
Vf²= 2.g.h (ma- µmb/ma+mb)
Eq. horária da velocidade – 0 = Vf – µg.t
Eq. horária da distância – x = Vf . t – µg. t²/2
0 = Vf – µg. t
t = Vf/ µ.g
x = Vf.t – µg. t²/2
x= Vf . Vf/ µ.g – µ.g. (Vf/ µ.g)²/2
x= Vf²/ µ.g – µ.g. Vf²/( µ.g)²/2
x= Vf²/ 2µ.g
substituindo o Vf²…
x= Vf²= 2.g.h(ma- µmb/ma+mb)/2µ.g
x= h/µ (ma- µmb/ma+mb)
Depois substituímos a velocidade final do primeiro movimento na inicial do segundo movimento:
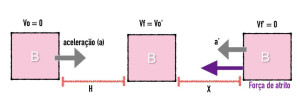
V²=2.ah
0²=Vo²-2a’.x
0=2ah-2a’x
a’=x/ah(cinemática)
Reescrevemos a equação para esta ficar em função de ma, mb, x e h
µ=ma.h/(ma+mb)x +mb.h
Colocamos a aceleração da queda em função de h e t. Essa será nossa aceleração teórica.
a(teorica)=2h/t²
O valor da aceleração teórica(cinemática) será comparada com a aceleração do experimento(dinâmica) em cada uma das duas acelerações a e a´.
ANÁLISE E CÁLCULOS
1) Cálculo do µ
µ=ma.h/(ma+mb)x +mb.h
[(85+-1).(460+-1)/([85+-1)+(105+-1)] (542+-) + (105+-1)(460+-1)
(39100+545)/(190+-2)(542+-4) +(48300+-565)
(39100+545)/(102980+-2844) + (48300+-565)
(39100+-545)/(151280+-2409)
µ=0,2585+-0,0077
2) Cálculo da 1ª aceleração a
- a(teórica-cinemática) = 2h/t²
h=0,46+-0,01
t=0,432+-0,01
2(0,46)/(0,432)²
0,92/0,186624=4,9296982167
erro:2(+-0,01)/(+-0,01)² = (+-0,02)/(0,00864) = (+-0,03356150855)
a=4,930+-0,336 m/s²
- a(experimental-dinâmica)= g(ma-µmb)/ma+mb
9,8[(85+-1)-(0,2585+-0,0077)(105+-1)/(885+-1)+(105+-1)
9,8[(85+-1)-(27,1425+-1,1067)/190+-2
9,8(57,8575+-2,1067)/190+-2
566,9545+-20,64566/190+-2
a=2,984+-0,031 m/s²
3) Cálculo da 2ª aceleração a´
- a´(experimental-dinâmica) = µ.g
(0,2585+-0,0077).9,8
a´= 2,533+-0,075 m/s²
- a´(teórico-cinemática) = x/a.h
x=0,542+-0,004 m
h= 0,46 +- 0,01 m
a= 4,930+- 0,336 m/s²
0,542/4,930.(0,46) = 0,0505720081 = 0,0506
erro: +-0,004/(+-0,01).(+-0,336) = +-0,0232481535 = +-0,023
a´= 0,0506+-0,023 m/s²
Comparando os resultados, observamos que:
- Há diferenças significativas entre os valores de cada uma das acelerações, isso deve-se ao fato de haver erros em cada medição e fatores foram desconsiderados como a superfície dos materiais, o que poderia gerar mais atrito, influenciando nos resultados, além da imprecisão das medidas, levando a arredondamentos, que acabam diferindo os resultados.

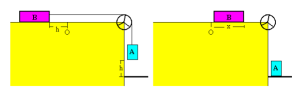
![WP_20150716_005[1]](http://aprendendofisica.net/rede/files/2015/08/WP_20150716_0051-300x169.jpg)