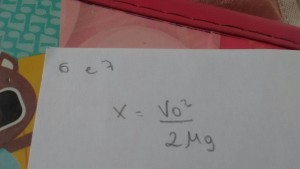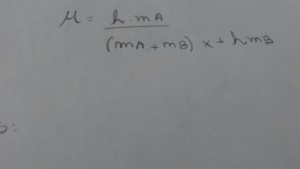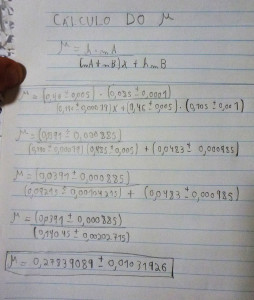Experimento no Laboratório – Projeto de Aprendizagem #2 (2015)

Publicado em 16/08/2015 por

Colégio Pedro II – Campus Centro

Turma 1205, 2º ano – 2015

Professor: Sérgio Lima

Alunas:

Beatriz Salazar – 05

Juliana Torres –16

Nathalia Hermes – 29

 

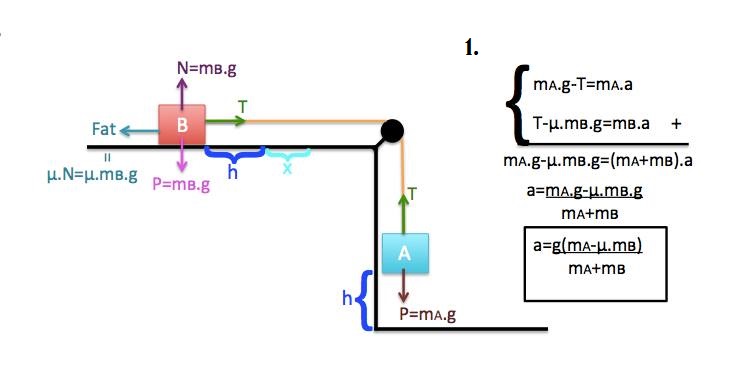
O experimento

fis2

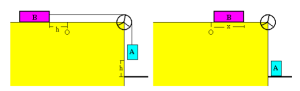
Consiste na análise dos seguintes acontecimentos: existem dois blocos na superfície de uma mesa, sendo esses os blocos A e B. O bloco B, por ser mais pesado, possui um peso sobre ele, de forma que o sistema permaneça parado; já o bloco A fica pendurado por uma corda.

O experimento tem início ao, após termos anotado os valores predispostos, retirarmos o peso de cima do bloco B e, assim, o outro bate no chão, enquanto o tempo é devidamente cronometrado. De acordo com Newton, um corpo em movimento tende a permanecer em movimento (ref. 1ª lei de Newton), que é o que acontece com o bloco B, que ainda percorre certa distância.

O objetivo é que, a partir dos dados colhidos e dados, identifiquemos velocidade, aceleração, coeficiente de atrito e equações do Movimento Uniformemente Variado, dentre outros pormenores que envolvem essas mesmas questões.

fis1

Dados

h – altura/distância entre o bloco A e o chão e, consequentemente, parte da distância percorrida pelo bloco B: 46,5 ± 0,1 cm

x – a distância restante percorrida pelo bloco B: 59 ± 0,1cm

t – tempo que o bloco B leva para alcançar o chão: 0,438s

ma – massa do bloco A: 85 ± 1g

mb – massa do bloco B: 105 ± 1g

 

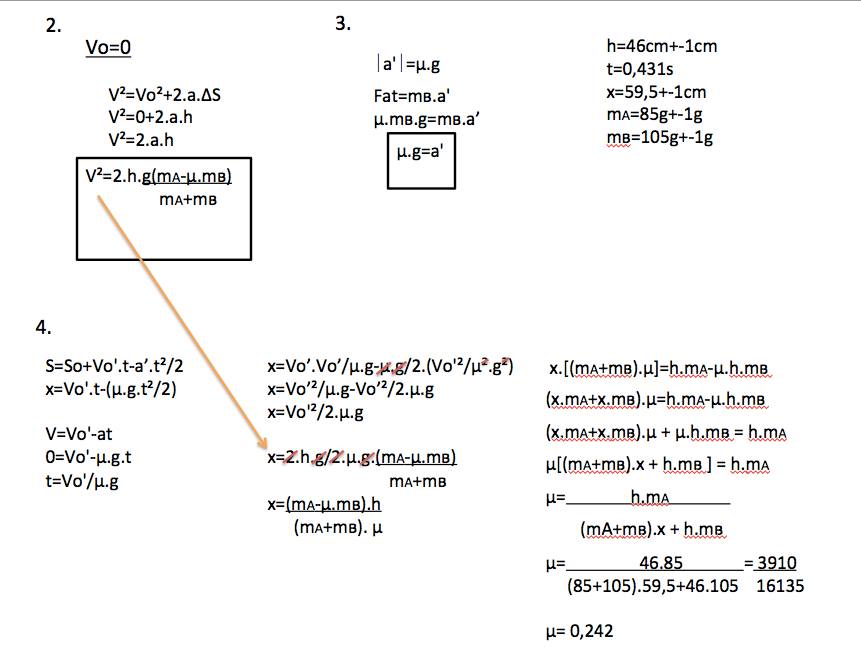
Cálculos

 

Coeficiente de atrito:

μ =     ma.h

–––––––––––––––

(ma + mb)x + mb.h

 

μ =                             (85 ± 1).(46,5 ± 0,1)

––––––––––––––––––––––––––––––––––––––––––––

[(85 ± 1) + (105 ± 1)].(59 ± 0,1) + (105 ± 1).(46,5 ± 0,1)

 

 

μ =                 3952,5 ± 55

–––––––––––––––––––––––––––

(190 ± 2).(59 ± 0,1) + (4882,5 ± 57)

 

 

μ =                3952,5 ± 55

–––––––––––––––––––––––––––

(11210 ± 137) + (4882,5 ± 57)

 

μ =   3952,5 ± 55

–––––––––––––

(16092,5 ± 194)

 

μ = 3952,5 ± 55       (   55       3952,5.194 )

–––––––––– +   (––––– + ––––––––––– )

16092,5             (16092   (16092,5)² )

 

μ = 0,246 ± 0,003 + 0,003

 

μ = 0,246 ± 0,006

 

Aceleração real:

a =   (ma – μ.mb)

(–––––––––––) . 9,8

( ma + mb )

 

 

a =   (85 ± 1) – [(0,246 ± 0,006).(105 ± 1)]

–––––––––––––––––––––––––––––––––       . 9,8

(85 ± 1) + (105 ± 1)

 

 

a =   [ (85 ± 1) – (25,83 ± 0,872)   ]

[–––––––––––––––––––––––––] . 9,8

[               (190 ± 2)               ]

 

a =   (59,17 ± 1,876)

(–––––––––––– ) . 9,8

(       190 ± 2   )

 

a =   [   59,17 ± (1,87 + (59,17.2) ) ]

[–––––––     ( ––––   (––––––) ) ] . 9,8

[     190     ( 190   ( 190)²) ) ]

 

a = (0,311 ± (0,01 + 0,003)).9,8

a = (0,311 ± 0,013).9,8

a = 3,048 ± 0,127

a= 0,03048±0,00127m/s²

 

 

Velocidade de B quando A toca o chão:

V² = 2.(3,048 ± 0,127).(46,5 ± 0,1)

V² = 2.(141,732 ± (5,906 + 0,305))

V² = 2.(141,732 ± 6,211)

V² = 283,464 ± 12,422

V = √283,464 ± 12,422

 

Agora, trabalhando isoladamente com o seguinte modelo:

x

–––––– = a ± b

a ± b

 

x = (a ± b).(a ± b)

x = a² ± 2ab

√(a² ± 2ab)

 

Aplicando isso na descoberta de V, temos que:

√283,464 ± 12,422 = √(a² ± 2ab)

283,464 = a²

a = √283,464 => a = 16,836 //

12,422 = 2ab

33,642b = 12,422

b = 0,369

Logo, V = 16,836 ± 0,369 => V = 0,168 ± 0,00369m/s

 

 

Dedução de a’:

μ . g = a’ è g experimental

a’ =(0,246 ± 0,006).10

a’ = 2,46 ± 0,06

a’=0,0246±0,0006m/s²

 

Equações do MUV para B (após o bloco A tocar o chão):

0² =0,438 ± 0,001 + 2.a.(59 ± 1)

0 = 0,438 ± 0,001 + (118 ± 2).a

-(0,438 ± 0,001) = (118 ± 2).a

a =     (0,438 ± 0,001)

– –––––––––––––

(118 ± 2)

 

a = [0,438     (0,001   (0,438.2) )

  • [––––– ± (–––– + (–––––––))

[ 118      ( 118     (   118² ))

 

a = – 0,004

a= – 0,00004m/s²

 

 

S = S0 + V0t + at²

––––

2

59 ± 1 = 0,438 ± 0,001 ± a.(0,438 ± 0,001)²

–––––––––––––––––––––––––––––––

2

59±1=0,438±0,001+a.0,095922±0,001

58,562±1,001=a.0,095922±0,001

a=6,1±0,17m/s²

 

Comparativamente, ao observar as acelerações, podemos perceber que o erro é maior quando se utiliza dados teóricos. Isso ocorre porque os valores não são tão maleáveis quanto tudo que se mede durante o experimento

Publicado em Física | 1 Comentário

Relatório do Experimento de Força de Atrito.

Publicado em 16/08/2015 por

Colégio Pedro II – Campus Centro 

Disciplina: Física     Professor: Sérgio

Turma: 1201

Grupo:

Beatriz Torreão – nº: 4

Gabriel Fiami – nº: 10  

Gabriel Almeida – nº: 11

Victor Magalhães – nº: 29

 

Objetivo:

Achar o coeficiente de atrito cinético da mesa em que o bloco B encontrava-se, foi o propósito desse experimento.

O fenômeno físico do experimento:

No colégio, no experimento em que fizemos, tínhamos dois blocos unidos por uma corda de massas distintas, os quais chamamos de A e B. O bloco que ficava sobre a mesa era o B e o que estava, a princípio pendurado, o A. Posicionamos, no começo, um peso sobre B para verificar os intervalos entre os blocos e o intervalo do bloco A até o chão. Assim que o peso foi removido do bloco B, o bloco A desabou no chão, movendo o bloco B pela distância H, que é o intervalo de A ao chão. E esse bloco se movimentou, além dessa distância H, uma distância X , no decorrer de T segundos.

Análise Experimental:

As medidas obtidas durante o experimento foram as com os seguintes valores:

H= 0,46m +/- 0,005m                                                                                                                                                                            X= 0,485m +/- 0,005m                                                                                                                                                                          mA= 0,085kg +/- 0,001kg                                                                                                                                                              mB= 0,105kg +/- 0,001kg

Tempo= 0,417s.

Pré-análise:

Aqui segue a montagem e a escolha de algumas fórmulas físicas para o cálculo final do valor do coeficiente de atrito:

1- Aceleração teórica.

Fisica1

 

2- Velocidade que o bloco B toca o chão.                                                                                                                                             e                                                                                                                                                                                                                3- Aceleração Teórica

Fisica2

4 e 5 – M.U.V.

Fisica3

6- Fórmula para X.

Fisica4

7- Fórmula para o coeficiente de atrito.

Fisica5

Cálculo do coeficiente de atrito cinético:

Após a pré-análise, temos informações que nos permitem fazer o cálculo do coeficiente de atrito cinético da mesa. Segue na imagem a seguir, o cálculo:

P1120260

 

No término do cálculo encontramos que o Coeficiente de atrito cinético da mesa = 0,27839089 +/- 0,01031926.

 

Publicado em 2-ano, 2015, 2102, Física | 1 Comentário

Relatório do experimento da 2º certificação

Publicado em 16/08/2015 por

Colégio Pedro II – Campus Centro

Disciplina: Física

Professor: Sérgio Lima

Grupo: Bernardo Maia       Nº: 6

Breno Cipolatti       Nº: 7

Felipe Pais               Nº: 9

José Victor               Nº: 17

AlJsgdtnvKUb2dYKRoWgJcD7Mzns1Ydwo8MjY_SxOczp

 

No dia 16/07 a turma fez um experimento no laboratório de física, com a intenção de examinar fenômenos que consistem em velocidade, peso, atrito e aceleração.

Foram usados objetos comuns, como blocos de madeira, linha e um pequeno peso de ferro, também foi utilizado um equipamento eletrônico, um cronometro de alta precisão, que era composto pelo mostrador (onde mostra o tempo) e dois “retângulos” vazados que contêm um laser cada, que inicia e para o cronometro quando um objeto passa por eles.

Devemos descobrir o coeficiente de atrito cinético, comparar a aceleração teórica com a experimental e analisar a propagação de erros no experimento.

 

kbj

 

O primeiro passo é descobrir a aceleração teórica. Para isto, deve-se usar os seguintes passos:

Fat = μ · N      ou      Fat = μ · Mb · g

Ma · g – T = Ma · a             +

T – μ · Mag = Mb · g

Ma · g – μ · Mb · g = (Ma + Mb) a

a = Ma · g – μ · Mb · g    —–>   (Ma – μ · Mb) · g

Ma + Mb                                     Ma + Mb

Agora é só substituir pelos números dados.  Porém ainda necessitamos descobrir μ (coeficiente de atrito), em uma conta separada.

Devemos usar a fórmula: 

zdnzfh

μ = (0,085 ± 0,001 · 0,457 ± 0,01)/(0,085 ± 0,001 + 0,105 ± 0,001) · 0,504 ± 0,01 + 0,105 ± 0,001 · 0,457 ± 0,01

μ = 0,039 ± 0,0013/(0,190 ± 0,002 · 0,504 ± 0,01) + (0,105 ± 0,001 · 0,457 ± 0,01)

μ = 0,039 ± 0,0013/0,096 ± 0,003 + 0,048 ± 0,0015

μ = 0,039 ± 0,0013/0,144 ± 0,0018

μ = 0,27 ± 0,0125

Feito isso, só substituir as letras por números:

Fat = μ · N     ou      μ · Mb · g
Fat= 0,27 ± 0,017 · 105 ± 1 · 9,8

Ma · g – T = Ma · a            +

T – μ · Mb · g = Mb · a

0,085 ± 1 · 9,8 – T = 0,085 ± 1 – a

T – 0,27 ± 0,017 · 0,105 ± 1 · 9,8 = 0,105 ± 1 · a

(0,085 ± 0,001 · 9,8) – (0,27 ± 0,0073 · 0,105 ± 0,001 · 9,8) = ( 0,085 ± 0,001 + 0,105 ± 0,001) · a
( 0,085  ± 0,001 · 9,8) – ( 0,27 ± 0,0073 · 0,105 ± 0,001· 9,8) = 0,190 ± 0,002 · a

 

a = ( 0,085 ± 0,001 · 9,8) – ( 0,27 ± 0,0073 · 0,105 ± 0,001 · 9,8)

0,190 ± 0,002

a = 9,8 ( 0,085 ± 0,001 – 0,27 ± 0,0073 · 0,105 ±  0,001)
0,190 ± 0,002

a = 9,8 ( 0,085 ± 0,001 – 0,028 ± 0,001)

0,190 ± 0,002

a = 9,8 (0,057 ± 0,002)

0,190 ± 0,002

a = 0,56 ± 0,002 

0,190 ± 0,002

a =  2,95 ± 0,041   m/s²

Esta aceleração está em função das massas

Agora, deve-se descobrir a aceleração experimental:

a = 2h /t²

a = (2 · 0,457 ± 0,01)/(0,410 ± 0,01)²

a = 0,914 ± 0,01/0,17 ± 0,0001

a = 5,38 ± 0,063 m/s²

Foi observado que a aceleração experimental foi maior que a teórica.

Agora, deve-se descobrir a velocidade de do bloco B quando o bloco A toca o chão. Para isto, devemos usar a equação de Torricelli, com as duas acelerações:

   Vf² = Vo² + 2 · a · ΔS
Vf² = 2 · H · a

  Vf² = 2 · 45,7 ± 1 · 2,95 ± 0,041                                               Vf² = 2 · 45,7 ± 1 · 5,38 ± 0,063

   Vf² = 91,4 ± 1 · 2,95 ± 0,041                                                    Vf² = 91,4 ± 1 · 5,38 ± 0,063

   Vf² = 269,6 ± 6,7                                                                        Vf² = 491,7 ± 11,1

   Vf   = √269,6 ± 6,7                                                                      Vf = √491,7 ± 11,1

Agora que descobrimos a velocidade em que o bloco B percorre a distancia H, devemos, usando as leis de Newton, descobrir a aceleração dinâmica, que é a aceleração que o bloco B tem após o bloco A tocar o chão, em função de μ e Mb: 

   Aceleração dinâmica:                                                                 Aceleração cinemática:

Fr = Fat
μ ·Mb · g = Mb · a’                                                                              a’ = x/a.h

a’ = μ · g                                                                                                a’ = 0,504 ± 0,01/5,38 ± 0,063 · 0,457 ± 0,01

a’ = (0.27 ± 0,0073) · 9,8                                                                  a’ = 0,504  ± 0,01/2,46 ± 0,082

a’ = 2,65 ± 0,0073 m/s²                                                                      a’ = 0,2 ± 0,01 m/s²

A aceleração dinâmica foi bem maior que a cinemática.

Em seguida, usando as equações do MUV para a massa até parar percorrendo a distância x:

Δ S= Vo · T – a‘T²/2

X = Vo · T – μgT²/2

Agora devemos isolar o T da equação da velocidade e substituímos na equação de posição:

 

V = Vo – aT

0=  Vo – μgT

Vo = μgT

T =  Vo/ μg

                                                                                              
X= Vo · Vo/μg – μg/2 · (Vo/μg)²

X= Vo · Vo/μg – μg/2 · Vo²/μ² g²

X= Vo²/μg  – Vo²/2μg

X= Vo²/2μg

 

X=        Vo² / 2 · 0,27 ± 0,0073 · 9,8

 

Vo² = Vf², pois a velocidade que ele começa a percorrer o espaço X é a mesma que ele termina de percorrer o espaço H. Entã só devemos substituir Vo² pela fórmula do Vf²:

X =   2 · H · a  /2μg

X =   2 · H · a  /2μg                                                                          Obs:    a = (Ma – μ · Mb) · g / (Ma + Mb)

X =  H · [(Ma – μ · Mb) · g /(Ma + Mb)] / μg

X =    H · [(Ma – μ · Mb) · g/(Ma + Mb)] / μg

X =    H · [(Ma – μ · Mb)/(Ma + Mb)] / μ

Xμ =  H · (Ma – μ · Mb)/(Ma + Mb)

(Ma + Mb) · Xμ =  H · (Ma – μ · Mb)

(Ma + Mb) μX = HMa – Hμ·Mb

(Ma + Mb) μX + Hμ·Mb = HMa

Xμ + Hμ·Mb = (HMa)/(Ma+ Mb)

μ (X + HMb) = (HMa)/(Ma+ Mb)

μ = (HMa)/(Ma + Mb)X + HMb

Publicado em 1201, 2-ano, 2015, Experimentos, Projetos, Projetos-Aprendizagem | Deixe um comentário

Análise do experimento de fisica

Publicado em 16/08/2015 por

Rio de Janeiro, 15 de agosto de 2015

Colégio Pedro II-Campus Centro

Alunas: Ana Beatriz Santos, Anna Carolina Alkimin, Letícia Helena Real, Luiza Barreto e Luiza Siqueira

T: 1205       nos: 01, 02, 18, 23 e 24

O experimento: No dia 16 de Julho de 2015 realizamos um experimento, no laboratório de física, onde observamos em cima da mesa um bloco B ligado a um bloco A (como na foto abaixo). Quando o peso que estava no bloco B era retirado de cima dele o bloco A caia, percorrendo uma distância h enquanto o bloco B percorria ao mesmo tempo a mesma distancia h com a mesma aceleração do bloco A. Mas após percorrer a distância h, o bloco B ainda percorria uma distância x freando (a’). No laboratório medimos h, x, t e as massas do bloco B e A já tinham sido medidas anteriormente pelo professor e com essas medidas fomos capazes de deduzir µ e a aceleração com seus respectivos erros.

1 . Usando as Leis de Newton deduzimos a em função de ma , mb e g.

 

11880300_884703774932949_852061449_n

 

2 . Usando a equação de Torricelli deduzimos a velocidade do blocoB quando blocoA toca o chão.

3 . Usando as Leis de Newton para deduzimos a’ em função de mb e μ.

4 . Usamos a equação do M.U.V. para descobrirmos x percorrido por B até parar. Em seguida reescrevemos a equação de modo que μ fique em função de ma , mb , x e h.

 

11868885_884703781599615_1188246840_n

 

5 . Deduzimos a expressão da aceleração de queda em função de h e t (a experimental) comparado com a teórico. *

11880073_884875311582462_1945014636_n

*A diferença entre a aceleração teórica para experimental pode ser explicada pelo fato de que o cálculo da aceleração teórica não leva em consideração as possíveis interferências no experimento (real). Na teoria, por exemplo, alguns fatores podem ser considerados constantes ou não são considerados, enquanto na prática não temos como administrar isso, como a resistência do ar.

 

6 . Usando as regras de propagação de erro para determinamos o erro de μ em função dos erros de x, h, ma e mb.

11880874_884719598264700_1679023430_n

Publicado em 1205 | 1 Comentário