Colégio Pedro ll – Campus Centro
Christopher Brandão n°03
Gabriel Pais n°10 Turma: 1203
Luiz Arêdes n°25 Professor: Sérgio Lima
Paulo Marconi n°28
Introdução:
O experimento que fizemos em laboratório consiste num arranjo de dois blocos “A” e “B” (que possuem massas diferentes) são interligados por uma corda que passa por um sistema de roldana onde possibilita que ambos os blocos estejam presos um ao outro. O bloco “A” tinha um pequeno peso sob ele que o mantinha em equilíbrio com “B”, ao removê-lo, os dados do experimento puderam ser obtidos. Durante o experimento foi medido o tempo que o bloco A, que estava na mesa, demorou a percorrer entre dois pontos predeterminados e contamos com o auxílio de réguas e cronômetro para averiguar os resultados dos dados. Em seguida, nos foi dada a tarefa de determinar através de cálculos o μ (coeficiente de atrito do bloco que se arrastou pela mesa), e sua aceleração, para que depois pudéssemos calcular a margem de erro. A seguir os cálculos que fizemos com base nas equações fornecidas em sala pelo professor:
Ma= 85g +- 1g
Mb=105g +-1g
H=46 cm -> 0,460m
X=55,2cm -> 0,552m
T=0,407s/0,456s/0,407s
g=9,8m/s²
a’= μ. 9,8
a=10(85-μ . 105)/85 + 105
Vf =2 . 9,8 . 0,46(85- μ . 105/85+105)
0,552= Vf²/2. Mi.9,8
μx=85.0,46/(85+105).0,552+105
0,552=0,46/μ(85- μ105/85+105 . 0,46)
μ x= 39,1/15318= 0,255
Erro do A:
46 . 0,1 + 85 . 1= 89,6
Erro total das massas:
1+1=2
(Ma + Mb) . x -> 55,2 . 2 + 190. 0,1=129,4
a= 0,255 . 9,8
a= 2,499
= 2,5 +-1cm
Erro da multiplicação Mb . H
46 . 1 + 105 . 0,1 = 56,5
Erro entre a somas do denominador (ou erro do B)
129,4 + 56,5= 155,9
Erro da divisão
59,6/15318 + 3910/15318² . 185,9/1 = 234641,124
89,6/15318 + 0,0000166637 . 1859
0,0055493275+0,000016663=
0,0089471093
0,0089 aprox
Equação para a aceleração
a= 2H/T² -> 0,92/T²
0,92/0,165649 ->5,553m/s²
a= g(Ma – μ . Mb)/Ma + Mb
9,8 (85 – 0,255 . 105)/85-105
3,003m/s²
Erro da aceleração teórica
2 . 0,01= 0,002 0,02/0,407+0,92/(0,165649)²
T² -> (0,407 . 0,001) .2 0,1207372214+0,92/0,0279395412
0,00814
33,528196294 . 0,00814
0,1207372214+0,2729195178
0,3936567392m/s²
0,394m/s² aprox
Fotos









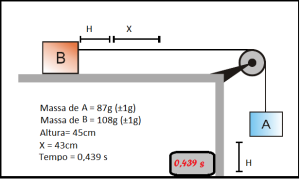
![IMG-20150814-WA0022[1]](http://aprendendofisica.net/rede/files/2015/08/IMG-20150814-WA00221-1024x767.jpg)